Séminaire informel de probabilités du DMA

14 octobre 2024. Igor Kortchemski (CNRS & DMA). Limites d'arbres aléatoires.
Nous esquisserons un panorama des limites de grands arbres aléatoires de Bienaymé-Galton-Watson

25 novembre 2024. Henri Orland (CEA IPTh). Chemins de transition de type ponts browniens et applications en biologie.

9 décembre 2024. Paul Gassiat (Dauphine & DMA). Titre à préciser.

27 janvier 2025. Thibaut Lemoine (Collège de France). Titre à préciser.

10 février 2025. Aurélien Garivier (ÉNS Lyon). Les projections aléatoires peuvent-elles être creuses ? Autour du lemme de Johnson-Lindenstrauss.
Les projections aléatoires constituent une technique de réduction de dimension simple et efficace en apprentissage automatique non supervisé. Elles reposent sur l'existence de quasi-immersions pour un ensemble de points d'un espace euclidien de haute dimension vers un espace de dimension inférieure. Nous proposerons une présentation du lemme de Johnson-Lindenstrauss centrée sur la notion de variable sous-gaussienne, puis nous discuterons de la meilleure manière de construire des projections simples, et en particulier creuses.

17 mars 2025. Eleanor Archer (Dauphine). Titre à préciser.

7 avril 2025. Antoine Jego (CNRS & Dauphine). Titre à préciser.

19 mai 2025.

2 juin 2025.

2 octobre 2023. Nathanael Enriquez. Du problème de l'arbre minimal au graphe d'Erdős-Rényi.
En guise d'introduction au graphe d'Erdős-Rényi, je présenterai une approche possiblement originale du célèbre problème initié par Alan Frieze du poids asymptotique de l'arbre couvrant minimal à l'intérieur d'un graphe complet dont les arêtes sont distribuées de façon iid. Le problème des fluctuations de ce poids conduira à quelques questions naturelles sur le graphe d'Erdős-Rényi, parmi lesquelles la limite du processus des fluctuations de la taille de la composante géante, lorsque le paramètre de connexion varie. (Travail conjoint avec Gabriel Faraud et Sophie Lemaire)

13 novembre 2023. Werner Krauth. Le TASEP lifté, exemple intégrable des chaînes de Markov non-réversibles.
Au cours des dernières années, les chaînes de Markov non-réversibles ont été à la base d'algorithmes de Monte Carlo puissants, puisque libérés de la condition du bilan détaillé. Dans cet exposé, je discuterai le TASEP (1) lifté (2), une chaîne de Markov à la fois proche des applications et intégrable par ansatz de Bethe. Le modèle décrit un système uni-dimensionnel de particules en interaction de sphères dures sur réseau. Ses propriétés étonnantes (partiellement comprises) rappellent celles des algorithmes ECMC (3) en dimension plus élevée. (1) TASEP: “Totally asymmetric simple exclusion process”, (2) lifté : “Lifted Markov chain, comme défini par Chen, Lovász et Pak (1999)”, (3) ECMC: “event-chain Monte Carlo”.

11 décembre 2023. Benoît Laslier. Le “solid on solid” penché est liquide, au moins quand on le dégivre un peu.
Le “solid on solid” (SOS) est un exemple classique de modèle effectif d'interface qui est supposé décrire la frontière entre deux phases dans le modèle d'ising 3D sous-critique ou plus généralement le bord d'un cristal. Il a été beaucoup étudié avec des conditions aux bords constantes mais toutes les surfaces ne peuvent pas être alignées avec le réseau cristallin ! Nous verrons que le modèle penché a un comportement très différent du cas classique : si ma température est suffisamment basse nous montrerons qu'il a de grandes fluctuations assymptotiquement décrite par un champ libre gaussien. Travail en collaboration avec Eyal Lubetzky.

8 janvier 2024. Max Fathi. Stabilité du trou spectral en courbure positive.
Un théorème de Lichnerowicz (1958) indique que pour les variétés riemanniennes en dimension n dont la courbure de Ricci est minorée par n-1, la plus petite valeur propre positive du Laplacien vérifie est minorée par n. Ce résultat a de nombreuses applications, y compris en probabilités (concentration de la mesure, comportement en temps long du mouvement Brownien). Cette borne est optimale, car il y a égalité pour la sphère. Elle a depuis été généralisée au cadre des espaces métriques mesurés à courbure positive. Dans cet exposé, je présenterai un résultat de stabilité, sur les variétés dont le trou spectral est presque minimal, et je parlerai du rôle des lois beta dans ce problème. Cet exposé ne nécessitera aucun prérequis de géométrie. Travail en collaboration avec I. Gentil et J. Serres.

5 février 2024. Denis Bernard. Limite en bruit fort d’équations stochastiques : Quelques leçons (ou questions) issues de modèles quantiques. Les effets de faibles bruits sur un système dynamique sont bien compris, et ont de nombreuses applications, aussi bien en mathématique qu’en physique. Ceux induits par de forts bruits le sont moins (à ma connaissance). Je discuterai le comportement des solutions de certaines équations stochastiques en bruit fort issues de la mécanique quantique. Ce sera l’occasion d’aborder et d’illustrer les notions d’observations récurrentes en mécanique quantique, de contrôle quantique, de trajectoires quantiques, et leur modélisation.

11 mars 2024. Yan Fyodorov. On the density of complex eigenvalues of sub-unitary scattering matrices. What is the density of eigenvalues for a finite-size diagonal block of a resolvent of a large random matrix, with the spectral parameter chosen in the vicinity of the real axis? I will explain how this mathematical question is motivated by real experiments in wave-scattering systems, where due to absorption the associated scattering matrix is sub-unitary, hence moduli of its eigenvalues are nontrivial. Then I will present the results for the mean density of those moduli in the framework of random matrix models of quantum chaotic scattering. Relations to the density of complex eigenvalues of GUE resolvent blocks and eventually to the density of resonance poles of the scattering matrix in the complex energy plane will be discussed and exploited.

25 mars 2024. Théo Lenoir. Graphes à décomposition modulaire prescrite, convergence au sens des graphons et nombre de sous-graphe induits. L'objectif de cet exposé est de montrer comment se comportent certains types de modèles de graphes en particulier des modèles de graphes à motifs exclus. Pour cela nous introduirons la décomposition modulaire, un outil relativement connu en algorithmique, mais dont l'étude d'un point de vue probabiliste a commencé très récemment. Nous verrons alors comment pour une large classe de modèles définies par diverses contraintes sur la décomposition modulaire, on arrive à connaître la densité de chaque graphe comme sous-graphe induit. Ce résultat implique une convergence au sens des “graphons” qui peut être vue comme une sorte de convergence des matrices d'adjacences. On a la convergence d'un graphe de taille n vers un graphe “continu” qui est appelé cographon brownien et peut être construit à partir d'une excursion brownienne.

22 avril 2024. Piet Lammers. The 2D XY model and its relation to height functions. In this talk, I will present a new way to view an old expansion of the XY model. This visual perspective allows us to build a link between the phase transition of the model and the phase transition of height functions. It is based on my recent preprint “Bijecting the BKT transition”. Only basic/general notions in probability theory will be assumed.

27 mai 2024. Antoine Mouzard. Mesures de Gibbs et quantification stochastique. Dans cet exposé, je présenterai l'étude de mesures de Gibbs en dimension infinie. Ces mesures sont issues de la théorie quantique des champs et peuvent être interprétées comme lois de champs stochastiques irréguliers. Il est alors possible de construire et d'étudier ces objets aléatoires grâce à des équations aux dérivées partielles stochastiques (EDPS) en général singulières.

3 juin 2024. Anna Erschler. La probabilité de retour sur des groupes de matrices triangulaires.

12 Juin 2023. Cyril Imbert. Autour des travaux de Krylov.

22 Mai 2023. Cyril Houdayer. Frontières de Poisson des marches aléatoires sur les groupes et rigidité pour les réseaux de rang supérieur.

17 Avril 2023. Jan Swart. Brownian net and Brownian web.

13 Mars 2023. Guilhem Semerjian. Introduction aux problèmes aléatoires de satisfaction de contraintes.

13 Février 2023. Clément Levrard. Inférence pour des données avec une structure persistante.

16 Janvier 2023. Anna Ben-Hamou. Les estimateurs par moyenne locale en régression non-paramétrique. On présentera des résultats classiques sur la convergence des estimateurs par moyenne locale en régression, en développant surtout l’exemple de l’estimateur des plus proches voisins.

12 Décembre 2022. Cristina Toninelli. Le modèle Est ou sur les surprises que l’on a quand on regarde seulement à droite.

7 Novembre 2022. Guillaume Dubach. Calcul de Weingarten. Soit $U$ une matrice unitaire aléatoire de taille $d*d$ distribuée selon la mesure de Haar (c'est à dire de manière uniforme sur le groupe unitaire $\mathrm{U}(d)$). Je décrirai une méthode pour borner (et au besoin, calculer exactement) l'espérance de n'importe quel monôme en les entrées de $U$. Cette méthode, qui découle de développements récents initiés par les travaux de Benoît Collins (2003), repose sur des fractions rationnelles en la dimension $d$, appelées fonctions de Weingarten en hommage à Donald Weingarten qui en calcula les premiers exemples (1978).

3 Octobre 2022. Quentin Berger. Influence du désordre dans des systèmes physiques. Je discuterai de la question de l’influence du désordre sur les transitions de phase de systèmes physiques, en particulier à travers l’exemple de certains modèles de polymères aléatoires.

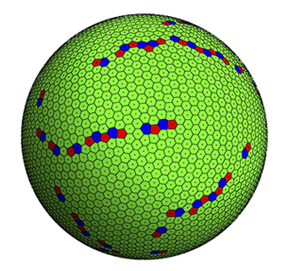
7 Juin 2022. Edward Saff. Discretizing Manifolds with Minimal Energy. Minimal discrete energy problems arise in a variety of scientific contexts, such as crystallography, nanotechnology, information theory, and viral morphology, to name but a few. The goal is to analyze the structure of configurations generated by optimal (and near optimal) N-point configurations that minimize the Riesz s-energy over a bounded surface in Euclidean space. The Riesz s-energy potential, which is a generalization of the Coulomb potential, is simply given by $1/r^s$, where r denotes the distance between pairs of points. We show how such potentials and their minimizing point configurations are ideal for use in sampling surfaces. Connections to the breakthrough results by Viazovska, Cohn, et al on best-packing and universal optimality in 8 and 24 dimensions will be discussed. Finally, we analyze the minimization of a k-nearest neighbor truncated version of Riesz energy that reduces the order $N^2$ computation for energy minimization to order $N\log N$, while preserving global and local properties.

31 Mai 2022. Carlo Mariconda. Le problème classique du calcul des variations: nouveaux résultats sur conditions nécessaires, régularité des minima et suites minimisantes.

24 Mai 2022. Gabriel Peyré. Introduction au transport optimal. Le transport optimal permet de définir des distances “géométriques” sur l'espace des distributions de probabilité. Il permet en particulier de quantifier la convergence en loi, qui est une notion de convergence faible utile à la foi en théorie (par exemple pour le théorème central limite) et en pratique (par exemple pour l'entraînement de réseaux de neurones). Dans cet exposé, je ferai un tour d'horizon de la formulation initiale de Monge et de sa relaxation sous la forme d'un problème convexe par Kantorovitch. Je mentionnerai le théorème de Yann Brenier qui fait le lien entre les deux. Enfin, je donnerai des exemples (en 1D, entre des nuages de points, entre des Gaussiennes) et j'esquisserai les limites théoriques et pratiques du transport optimal en grande dimension. Pour plus d'information (cours, slides, codes), vous pouvez vous rendre sur https://optimaltransport.github.io/

5 Avril 2022. Daniel Perez. Introduction à l'homologie persistante et à ses applications. L'homologie persistante est un invariant provenant de la topologie algébrique associé à un couple $(X,f)$ où $X$ est un espace topologique et $f : X \to \mathbb{R}$ est une fonction (continue). Ces invariants sont souvent utilisés en analyse topologique de données (TDA pour topological data analysis) et constituent un outil novateur dans l'appretissage statistique et dans l'analyse des données classique. Dans cet exposé, nous donnerons une introduction à l'homologie persistante, discuterons de ses applications et explorerons quelques conséquences de cette théorie sur l'étude des processus stochastiques sur des variétés Riemanniennes compactes.

8 Mars 2022. Giambattista Giacomin. Sur l’effet du désordre en mécanique statistique.
L’effet du désordre sur les modèles de la mécanique statistique est souvent surprenant (et, en tout cas, peu compris). J’approcherai ce problème avec le point de vue du « critère de (A. B.) Harris » et le but serait d’arriver à présenter les idées de base et de donner un panorama de ce qu’on (ne) sait (pas) faire. Note des organisateurs : pour en savoir plus, ne pas manquer les notes du cours de Saint-Flour 2010 de GB !

1 Février 2022. Guillaume Barraquand. Mesure de Schur, matrices aléatoires et systèmes de particules en interaction.
Les fonctions de Schur sont une base orthonormale de polynômes symétriques en plusieurs variables, qui possèdent de nombreuses propriétés combinatoires remarquables. L'une de ces propriétés, la formule sommatoire de Cauchy, permet de définir de manière très naturelle des mesures de probabilités sur les partitions d'entiers. Le but de l'exposé est d'expliquer une conséquence probabiliste de ces propriétés combinatoires, et son importance dans l'étude des processus de croissance d'interfaces, les systèmes de particules, ou encore les permutations aléatoires (d'après Baik-Deift-Johansson 1999, Johansson 2000, Okounkov 2001). Nous verrons au passage des liens surprenants avec la théorie des matrices aléatoires, et je conclurai en dressant un panorama des directions dans lesquelles ces résultats ont été généralisés pendant les 20 dernières années.

4 Janvier 2022. Dmitry Chelkak. Planar bipartite dimer model: discrete holomorphicity and Gaussian Free Field.
A classical theorem due to Kasteleyn says that the partition function of a planar dimer model equals to the Pfaffian of a properly signed adjacency matrix of the graph. In 2000, Kenyon proved that the fluctuations of the associated height function in special (so-called Temperleyan) discrete approximations to a given planar domain on refining square grids converge to the Gaussian Free Field. The starting point of Kenyon's argument is an interpretation of the Kasteleyn matrix as a discrete Cauchy-Riemann operator; one of the observations that brought discrete holomorphic functions to the focus of research on critical 2d lattice models during the following decade. However, the dimer model is known to be very sensitive to boundary conditions and such a straightforward interpretation fails for other types of discrete domains. One of the most classical examples of a more complicated behavior are the so-called Aztec diamonds: in this case, frozen/liquid zones appear and the height fluctuations in the liquid zone converge to a Gaussian field but the two-point function is not the standard Green function. The goal of this talk is to briefly review these classical results and – at the very end – to indicate recent developments on generalizations of the discrete complex analysis philosophy beyond “standard” setups.

7 Décembre 2021. Nathanaël Berestycki. Aperçu de la théorie conforme de Liouville.
La théorie conforme de Liouville a été introduite de manière non rigoureuse par Polyakov dans un papier fondamental de 1981. C'est une théorie quantique des champs (quantum field theory) en deux dimensions qui a une propriété supplémentaire d'invariance conforme, ce qui en fait une théorie conforme des champs. Je vais essayer de donner un aperçu de la construction rigoureuse de cette théorie donnée dans un papier tout aussi fondamental de David, Kupiainen, Rhodes et Vargas en 2015. Cette construction repose sur une version judicieusement choisie du champ libre Gaussien et sur son chaos multiplicatif Gaussien associé. J'essayerai également de montrer par un calcul simple en quoi cette théorie est « intégrable », c'est-à-dire qu'on peut espérer calculer de manière exacte un certain nombre d'observables. (Cette intégrabilité a notamment conduit Kupiainen, Rhodes et Vargas vers une preuve rigoureuse de la célèbre formule DOZZ).

9 Novembre 2021. Bastien Mallein. L'équation de convolution $P = P \ast Q$ de Choquet et Deny.

12 Octobre 2021. Raphaël Cerf. Le problème fondamental de la percolation en dimension 3.